Modul 3
MODUL 3
Hukum Ohm, Hukum Kirchhoff, Voltage & Current Divider, serta metode analisis Mesh, Nodal, dan Teorema Thevenin adalah konsep dasar dalam bidang teknik elektronika dan listrik yang digunakan untuk menganalisis dan merancang rangkaian listrik.
Hukum Ohm menyatakan hubungan antara tegangan, arus, dan resistansi dalam sebuah rangkaian listrik. Hukum Ohm menyatakan bahwa arus yang mengalir melalui suatu konduktor (seperti kawat) antara dua titik dalam suatu rangkaian listrik, berbanding lurus dengan tegangan listrik di antara kedua titik tersebut, dan berbanding terbalik dengan hambatan konduktor tersebut. Rumus matematisnya adalah V = I x R, di mana V adalah tegangan (Volt), I adalah arus (Ampere), dan R adalah hambatan (Ohm).
Hukum Kirchoff, terdiri dari Hukum Arus Kirchoff dan Hukum Tegangan Kirchoff, digunakan untuk menganalisis aliran arus dan tegangan dalam suatu rangkaian tertutup. Hukum Kirchoff terdiri dari dua hukum utama, yaitu Hukum Kirchhoff I (Hukum Arus Kirchoff) dan Hukum Kirchoff II (Hukum Tegangan Kirchoff). Hukum Arus Kirchoff menyatakan bahwa total arus yang masuk ke suatu simpul (node) dalam suatu rangkaian listrik sama dengan total arus yang keluar dari simpul tersebut. Hukum Tegangan Kirchoff menyatakan bahwa total penjumlahan tegangan dalam suatu lintasan tertutup (loop) dalam suatu rangkaian listrik adalah nol.
Voltage & Current Divider adalah teknik untuk membagi tegangan atau arus dalam rangkaian resistor yang terhubung seri atau paralel dalam rangkaian listrik. Voltage Divider digunakan untuk membagi tegangan listrik antara dua resistor dalam rangkaian seri, sedangkan Current Divider digunakan untuk membagi arus antara dua resistor dalam rangkaian paralel.
Metode analisis Mesh, Nodal, dan Teorema Thevenin adalah teknik matematis yang digunakan untuk menyederhanakan dan menganalisis rangkaian listrik yang kompleks.
Metode analisis Mesh digunakan untuk menganalisis rangkaian listrik dengan cara mendefinisikan arus yang mengalir dalam setiap loop tertutup dalam rangkaian dan menerapkan Hukum Tegangan Kirchhoff II. Metode analisis Nodal digunakan untuk menganalisis rangkaian listrik dengan cara mendefinisikan tegangan pada setiap simpul dalam rangkaian dan menerapkan Hukum Arus Kirchoff.
Teorema Thevenin menyatakan bahwa suatu rangkaian
listrik linier yang terdiri dari sumber tegangan (V) dan hambatan (R) dapat
digantikan oleh suatu sumber tegangan tunggal (Vth) dan hambatan tunggal (Rth)
jika dilihat dari dua titik terminal tertentu. Ini memudahkan analisis
rangkaian yang kompleks dengan menggantikan sebagian rangkaian dengan model yang lebih sederhana.
- Dapat memahami prinsip Hukum Ohm
- Dapat memahami cara kerja voltage dan current divider
- Dapat membuktikan arus dengan menggunakan Teorema Mesh
- Dapat membuktikan perhitungan tegangan degan menggunakan Analisis Nodal
- Dapat menentukan tegangan ekivalen Thevenin dan Resistansi Thevenin dari rangkaian DC
A. Alat
1. Instrument

Multimeter
2. Module



Module
3. Base Station

Base Station
4. Jumper

Jumper
B. Bahan

Resistor

Potensiometer
A. Resistor
Resistor merupakan komponen penting dan sering dijumpai dalam sirkuit Elektronik. Boleh dikatakan hampir setiap sirkuit Elektronik pasti ada Resistor. Tetapi banyak diantara kita yang bekerja di perusahaan perakitan Elektronik maupun yang menggunakan peralatan Elektronik tersebut tidak mengetahui cara membaca kode warna ataupun kode angka yang ada ditubuh Resistor itu sendiri.
Seperti yang dikatakan sebelumnya, nilai Resistor yang berbentuk Axial adalah diwakili oleh Warna-warna yang terdapat di tubuh (body) Resistor itu sendiri dalam bentuk Gelang. Umumnya terdapat 4 Gelang di tubuh Resistor, tetapi ada juga yang 5 Gelang.
Gelang warna Emas dan Perak biasanya terletak agak jauh dari gelang warna lainnya sebagai tanda gelang terakhir. Gelang Terakhirnya ini juga merupakan nilai toleransi pada nilai Resistor yang bersangkutan.
Tabel dibawah ini adalah warna-warna yang terdapat di
Tubuh Resistor :

Tabel Kode Warna Resistor
Perhitungan untuk Resistor dengan 4 Gelang warna :

Cara menghitung nilai resistor 4 gelang
Masukkan angka langsung dari kode warna Gelang ke-1
(pertama)
Masukkan angka langsung dari kode warna Gelang ke-2
Masukkan Jumlah nol dari kode warna Gelang ke-3 atau
pangkatkan angka tersebut dengan 10 (10n)
Merupakan Toleransi dari nilai Resistor tersebut
Contoh :
Gelang ke 1 : Coklat = 1
Gelang ke 2 : Hitam = 0
Gelang ke 3 : Hijau = 5 nol dibelakang angka gelang
ke-2; atau kalikan 105
Gelang ke 4 : Perak = Toleransi 10%
Maka nilai Resistor tersebut adalah 10 * 105 =
1.000.000 Ohm atau 1 MOhm dengan toleransi 10%.
Perhitungan untuk Resistor dengan 5 Gelang warna :
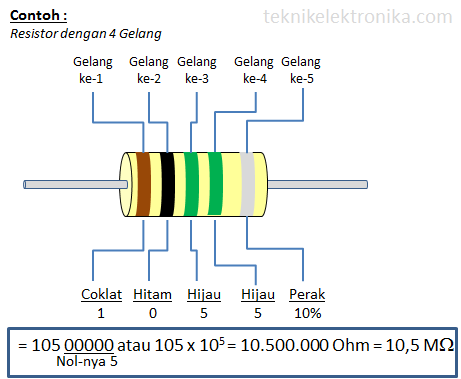
Cara Menghitung Nilai Resistor 5 Gelang Warna
Masukkan angka langsung dari kode warna Gelang ke-1
(pertama)
Masukkan angka langsung dari kode warna Gelang ke-2
Masukkan angka langsung dari kode warna Gelang ke-3
Masukkan Jumlah nol dari kode warna Gelang ke-4 atau
pangkatkan angka tersebut dengan 10 (10n)
Merupakan Toleransi dari nilai Resistor tersebut
Contoh :
Gelang ke 1 : Coklat = 1
Gelang ke 2 : Hitam = 0
Gelang ke 3 : Hijau = 5
Gelang ke 4 : Hijau = 5 nol dibelakang angka gelang
ke-2; atau kalikan 105
Gelang ke 5 : Perak = Toleransi 10%
Maka nilai Resistor tersebut adalah 105 * 105 =
10.500.000 Ohm atau 10,5 MOhm dengan toleransi 10%.
Contoh-contoh perhitungan lainnya :
Merah, Merah, Merah, Emas → 22 * 10² = 2.200 Ohm atau
2,2 Kilo Ohm dengan 5% toleransi
Kuning, Ungu, Orange, Perak → 47 * 10³ = 47.000 Ohm
atau 47 Kilo Ohm dengan 10% toleransi
Cara menghitung Toleransi :
2.200 Ohm dengan Toleransi 5% =
2200 – 5% = 2.090
2200 + 5% = 2.310
ini artinya nilai Resistor tersebut akan berkisar
antara 2.090 Ohm ~ 2.310 Ohm
B. Potensiometer
Potensiometer merupakan resistor variabel yang nilai resistansinya dapat diubah dengan cara memutar tuasnya untuk mendapatkan variasi arus. Potensiometer biasanya digunakan untuk mengendalikan perangkat elektronik. Salah satu contohnya seperti pengatur volume pada peralatan audio.
Potensiometer mempunyai 3 terminal, yaitu terminal A, terminal B, dan wiper. Dimana prinsip kerjanya ketika terminal A dan wiper dihubungkan maka nilai resistansinya semakin besar jika tuasnya diputar ke kanan. Ketika terminal B dan wiper dihubungkan maka nilai resistansinya semakin besar jika tuasnya diputar ke kiri. Sedangkan ketika terminal A dan B dihubungkan maka pada potensiometer akan menunjukkan nilai resistansi maksimum. Nilai resistansi ini akan selalu tetap dan merupakan nilai resistansi total dari potensiometer.



C. Hukum Ohm
Hukum Ohm pada dasarnya adalah hukum yang menjelaskan
mengenai kaitan antara tegangan atau beda potensial, arus listrik, serta
hambatan di dalam rangkaian listrik.
Jadi Hukum Ohm ini adalah hukum dasar yang menjelaskan
bahwa arus listrik yang mengalir pada suatu penghantar sebanding dengan
tegangan yang didapatkannya, tetapi arus berbanding terbalik dengan hambatan.
Arus listrik dapat mengalir melalui penghantar disebabkan karena adanya
perbedaan tegangan atau beda potensial yang ada di antara dua titik di dalam
penghantar.
Bunyi Hukum Ohm :
Bunyi hukum Ohm yang dipaparkan oleh George Simon
Ohm antara lain:
“Besarnya arus listrik yang mengalir pada suatu
penghantar akan sebanding dengan tegangannya, dalam suhu yang tetap.”
Dari pernyataan tersebut maka dapat dikatakan bahwa
perbandingan antara tegangan dengan arus listrik disebut dengan hambatan.
“Kuat arus yang mengalir dalam suatu penghantar atau hambatan besarnya sebanding dengan beda potensial atau tegangan antara ujung-ujung penghantar tersebut. Pernyataan itu bisa dituliskan sebagai berikut yaitu I ∞ V.” Hukum Ohm dirumuskan oleh fisikawan Jerman Georg Simon Ohm pada tahun 1827 dan dinyatakan dalam persamaan matematis sederhana:
V = I⋅R
V = tegangan dalam volt (V),
I = arus dalam ampere (A), dan
R = resistansi dalam ohm (Ω).
Hukum Ohm menyatakan bahwa tegangan pada suatu
komponen dalam suatu rangkaian sebanding dengan arus yang mengalir melaluinya,
dengan resistansi sebagai faktor proporsionalitasnya. Artinya, jika resistansi
tetap, maka arus dan tegangan akan memiliki hubungan linier. Jika resistansi
meningkat, arus akan menurun untuk mempertahankan proporsionalitas dengan
tegangan.
D. Hukum Kirchhoff
Hukum Kirchhoff ditemukan oleh Gustav Robert
Kirchhoff yang merupakan ahli fisika asal Jerman. Kirchhoff
menjelaskan hukumnya tentang kelistrikan ke dalam dua bagian, yaitu Hukum I
Kirchhoff dan Hukum II Kirchhoff.
Hukum I Kirchhoff
Hukum ini merupakan hukum kekekalan muatan listrik
yang menyatakan bahwa jumlah muatan listrik yang mengalir tidaklah berubah.
Jadi, pada suatu percabangan, laju muatan listrik yang menuju titik cabang sama
besarnya dengan laju muatan yang meninggalkan titik cabang itu. Nah, di fisika,
laju muatan listrik adalah kuat arus listrik. Oleh karena itu, bunyi Hukum I
Kirchhoff lebih umum ditulis:
"Jumlah kuat arus listrik yang masuk ke suatu
titik cabang akan sama dengan jumlah kuat arus listrik yang meninggalkan
titik itu."
Hukum I Kirchhoff biasa disebut Hukum Arus Kirchhoff
atau Kirchhoff’s Current Law (KCL).

Berdasarkan gambar diatas, besar kuat arus total yang melewati titik percabangan a secara matematis dinyatakan
Σ Imasuk = Σ Ikeluar
yang besarnya adalah
I1 = I2 + I3.
Hukum II Kirchhoff
Hukum ini berlaku pada rangkaian yang tidak bercabang
yang digunakan untuk menganalisis beda potensial (tegangan) pada suatu
rangkaian tertutup. Hukum II Kirchhoff biasa disebut Hukum Tegangan Kirchhoff
atau Kirchhoff’s Voltage Law (KVL). Bunyi Hukum II Kirchhoff
adalah:
"Jumlah aljabar beda potensial (tegangan) pada
suatu rangkaian tertutup adalah sama dengan nol."
Versi lain Hukum II Kirchhoff, yaitu pada rangkaian tertutup, berbunyi: jumlah aljabar GGL (ε) dan jumlah penurunan tegangan (IR) sama dengan nol. Secara matematis dapat dirumuskan sebagai:
Σ ε+Σ IR = 0

Berdasarkan gambar di atas, total tegangan pada rangkaian adalah Vab + Vbc + Vcd + Vda = 0. Hukum II Kirchhoff ini menjelaskan bahwa jumlah penurunan beda potensial sama dengan nol artinya tidak ada energi listrik yang hilang dalam rangkaian atau semua energi listrik diserap dan digunakan
Rangkaian pembagi tegangan
Rangkaian pembagi tegangan adalah suatu rangkaian
listrik yang dirancang untuk membagi tegangan input menjadi tegangan yang lebih
kecil pada beberapa resistor yang terhubung secara seri atau paralel. Prinsip
kerja dari rangkaian pembagi tegangan dapat dijelaskan dengan menggunakan hukum
Ohm dan aturan pembagian tegangan Kirchhoff.
Prinsip Kerja Rangkaian Pembagi Tegangan:
Resistansi Total (Rtotal): Rangkaian pembagi tegangan
terdiri dari dua atau lebih resistor yang terhubung. Resistansi total dari
rangkaian dapat dihitung dengan menggabungkan resistansi-resistansi tersebut
sesuai dengan koneksi (seri atau paralel).
Hukum Ohm: Hukum Ohm menyatakan bahwa arus dalam
rangkaian sebanding dengan tegangan dan invers sebanding dengan
resistansi. Dalam rangkaian pembagi tegangan, hukum Ohm digunakan untuk
menghitung arus pada rangkaian.
I = Vin/Rtotal
Aturan Pembagian Tegangan Kirchhoff: Aturan ini
menyatakan bahwa dalam suatu simpul (node) dalam suatu rangkaian listrik,
jumlah aliran arus menuju simpul tersebut sama dengan jumlah arus yang
meninggalkan simpul tersebut. Dalam rangkaian pembagi tegangan, aturan ini
diterapkan untuk simpul pada kedua ujung resistor pembagi.
Vin = V1 + V2 + ... + Vn
Dimana V1, V2, ..., Vn adalah tegangan pada masing-masing resistor.
Tegangan Keluaran (Vout): Tegangan keluaran pada titik
tertentu diambil dari resistor tertentu dalam rangkaian. Tegangan pada setiap
resistor dihitung dengan menggunakan aturan pembagian tegangan Kirchhoff.
Vout = Vin x (Rtarget/Rtotal)
Dimana Rtarget adalah resistansi resistor yang
terhubung pada titik keluaran.
Dengan memilih nilai resistansi yang sesuai, rangkaian pembagi tegangan dapat menghasilkan tegangan keluaran yang merupakan fraksi dari tegangan input.
Rangkaian pembagi arus
Rangkaian pembagi arus menggunakan sifat rangkaian
paralel, yaitu jumlah arus yang masuk sama dengan jumlah arus yang keluar dari
titik percabangan. Rangkaian pembagi arus membagi arus total yang masuk ke
dalam cabang-cabang rangkaian sesuai dengan perbandingan hambatan pada
masing-masing cabang. Rumus untuk menghitung arus pada cabang ke-n adalah:
In = I × Rn/Rtotal
Dimana In adalah arus pada cabang
ke-n, I adalah arus total yang masuk, Rtotal adalah
hambatan pengganti rangkaian paralel, dan Rn adalah hambatan pada
cabang ke-n.
F. Teorema Mesh

Gambar 4.3. Rangkaian Arus Mesh
Metode arus Mesh merupakan prosedur langsung untuk
menentukan arus pada setiap resistor dengan menggunakan persamaan simultan.
Langkah pertamanya adalah membuat loop tertutup (disebut juga mesh)
pada rangkaian. Loop tersebut tidak harus memiliki sumber tegangan, tetapi
setiap sumber tegangan yang ada harus dimasukkan ke dalam loop. Loop haruslah
meliputi seluruh resistor dan sumber tegangan. Dengan arus Mesh, dapat ditulis
persamaan Kirchoff’s Voltage Law untuk setiap loop.
G. Teorema Thevenin
Teorema Thevenin merupakan salah satu metode
penyelesaian rangkaian listrik kompleks menjadi rangkaian sederhana yang
terdiri atas tegangan thevenin dan hambatan thevenin yang terhubung secara
seri. Beberapa aturan dalam menetapkan Vth dan Rth,
yaitu:
1. Vth adalah tegangan
yang terlihat melintasi terminal beban. Dimana pada rangkaian asli, beban
resistansinya dilepas (open circuit). Jika dilakukan pengukuran, maka
diletakkan multimeter pada titik open circuit tersebut.
2. Rth adalah
resistansi yang terlihat dari terminal pada saat beban dilepas (open circuit)
dan sumber tegangan yang dihubung singkat (short circuit).
H. Analisis Nodal
Rangkaian analisis node saling melengkapi dengan
rangkaian analisis mesh. Rangkaian analisis node menggunakan hukum Kirchhoff
pertama, hukum Kirchhoff saat ini (KCL). Seperti yang kita sebutkan di atas,
namanya menyiratkan bahwa kita menggunakan tegangan node dan menggunakannya
bersama dengan KCL.
Analisis node mengharuskan kita untuk menghitung
tegangan node di setiap node sehubungan dengan tegangan ground (node
referensi), maka kita menyebutnya metode node-voltage.
Analisis node didasarkan pada aplikasi sistematis
hukum Kirchhoff saat ini (KCL). Dengan teknik ini, kita akan dapat menganalisis
rangkaian linier apa pun.
Apa saja yang perlu Anda persiapkan sebelum
menggunakan metode ini? Perlu diingat bahwa kita akan mendapatkan persamaan ‘n-1′,
di mana n adalah jumlah node termasuk node referensi. Menggunakan metode
analisis rangkaian ini berarti kita akan fokus pada tegangan node di rangkaian.
Sifat rangkaian analisis node:
- Rangkaian analisis node menggunakan hukum arus Kirchhoff (KCL)
- Untuk node ‘n‘ (termasuk node referensi) akan ada persamaan tegangan node independen ‘n-1′
- Memecahkan semua persamaan akan memberi kita nilai tegangan node
- Jumlah node (kecuali node non-referensi) sama dengan jumlah persamaan tegangan node yang bisa kita dapatkan.
.png)
Komentar
Posting Komentar